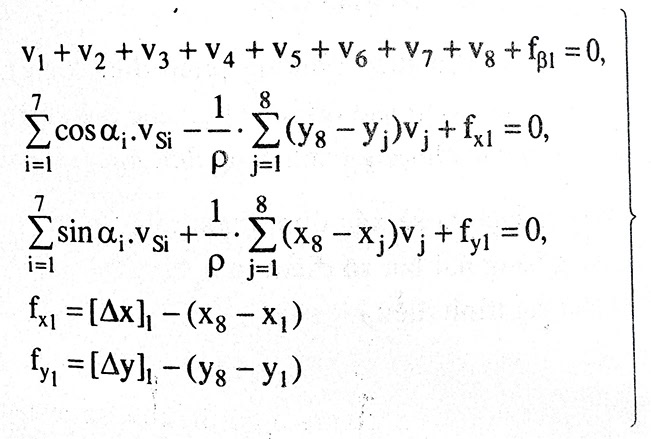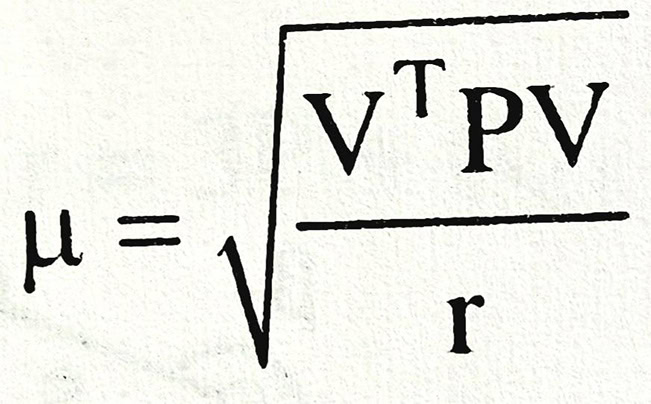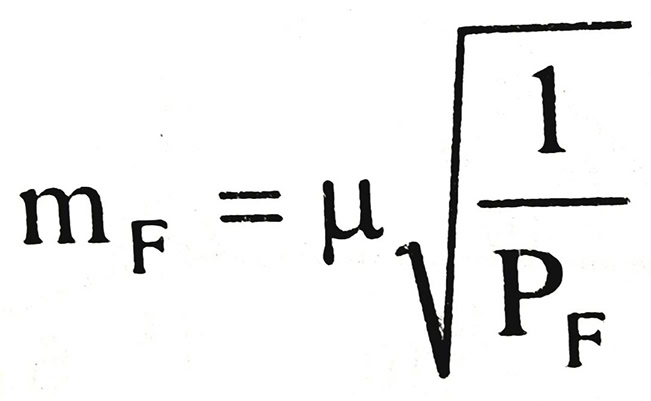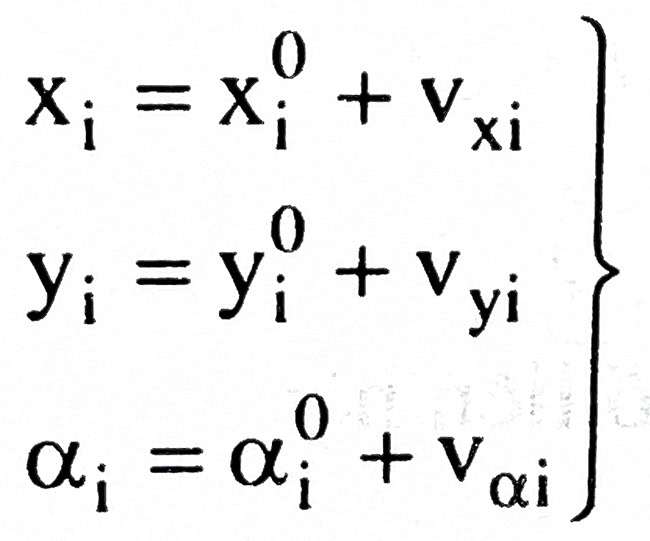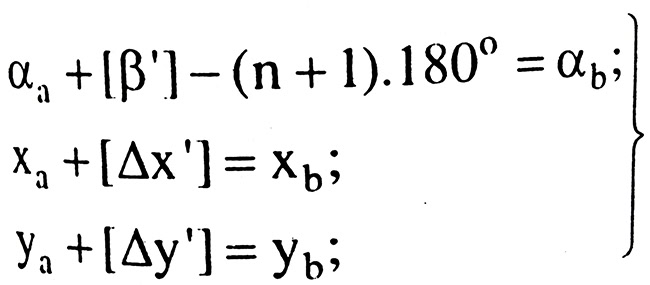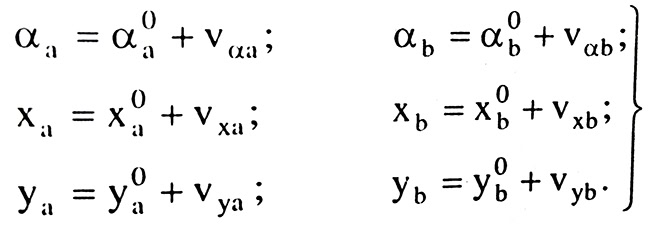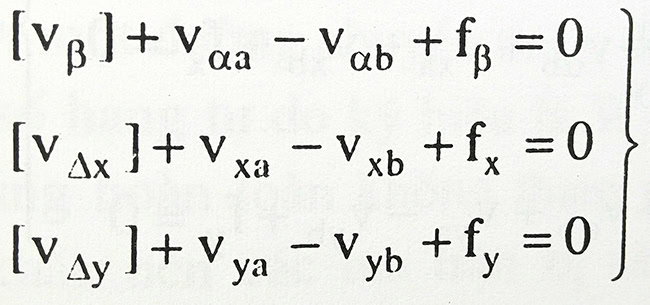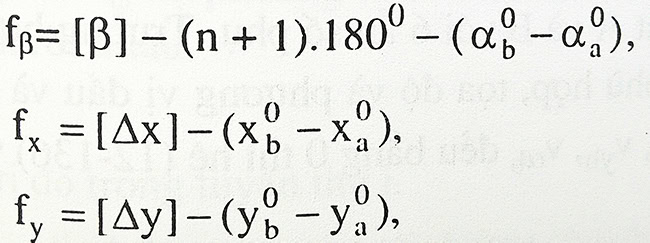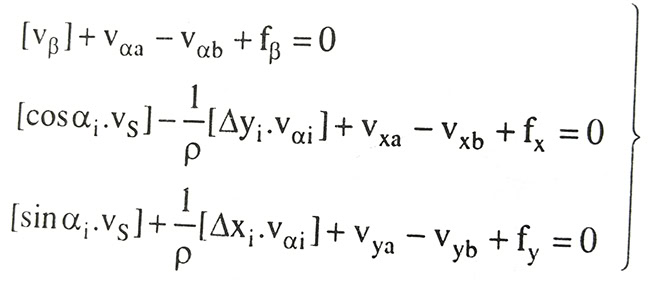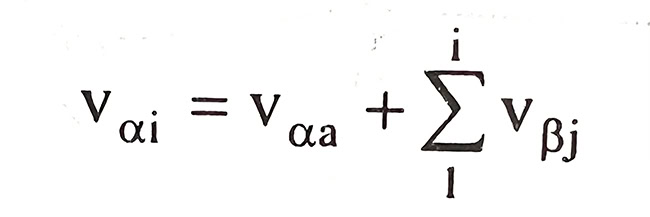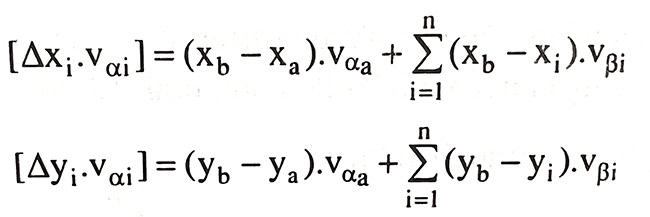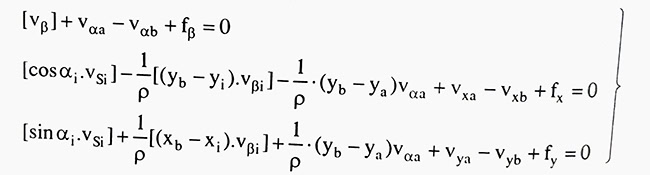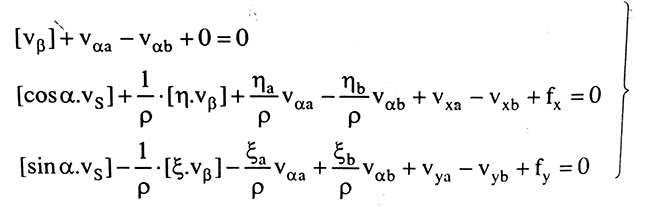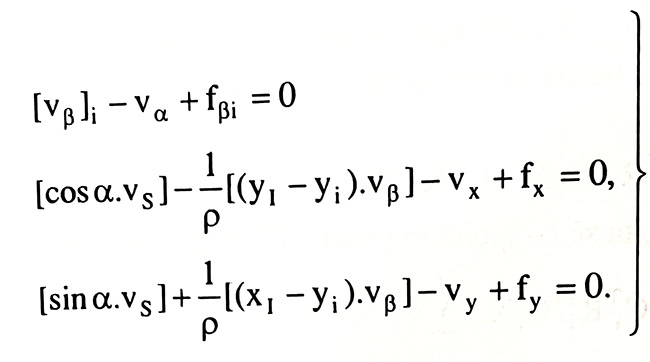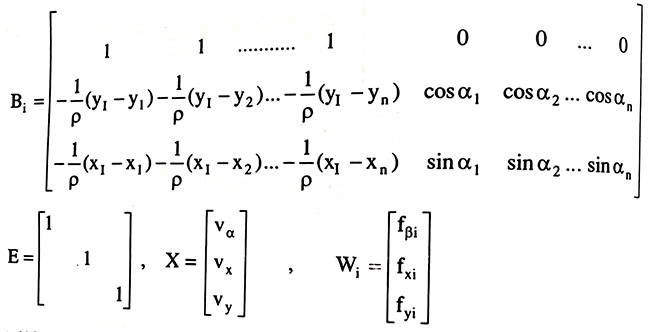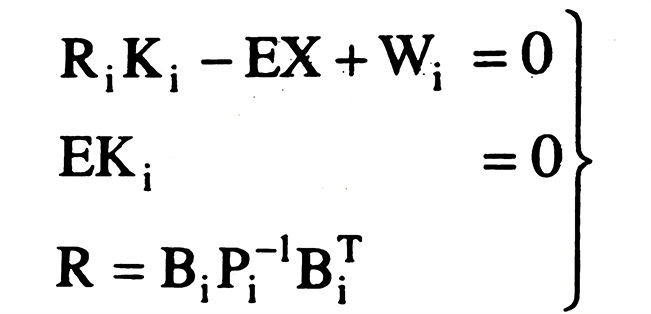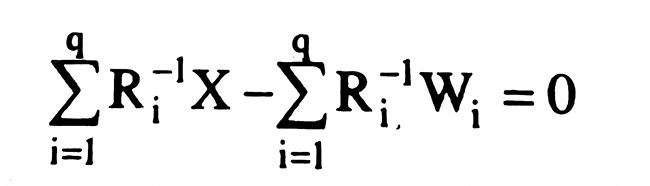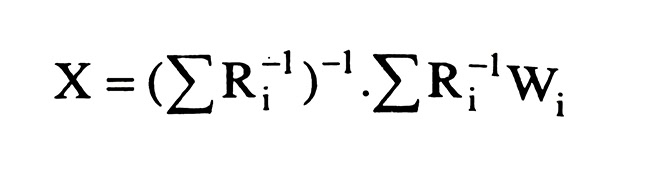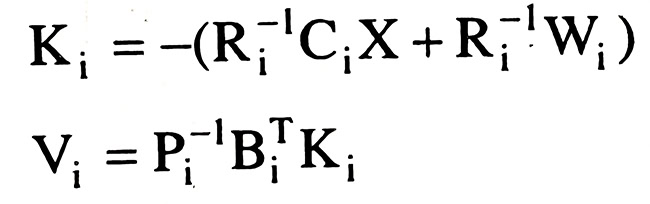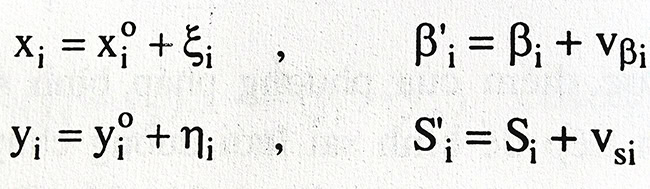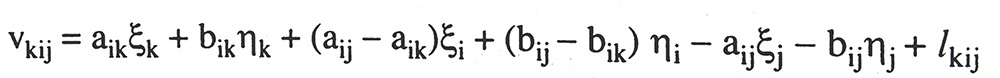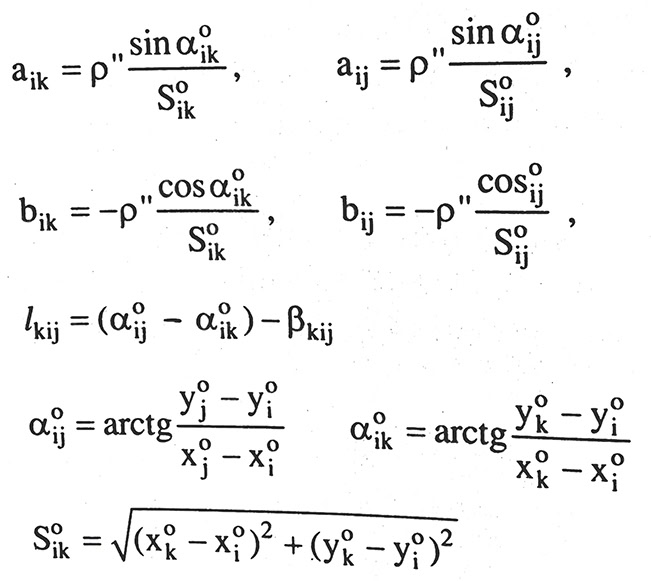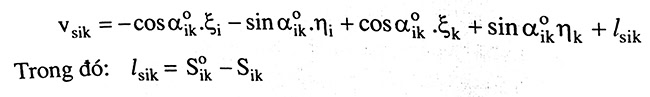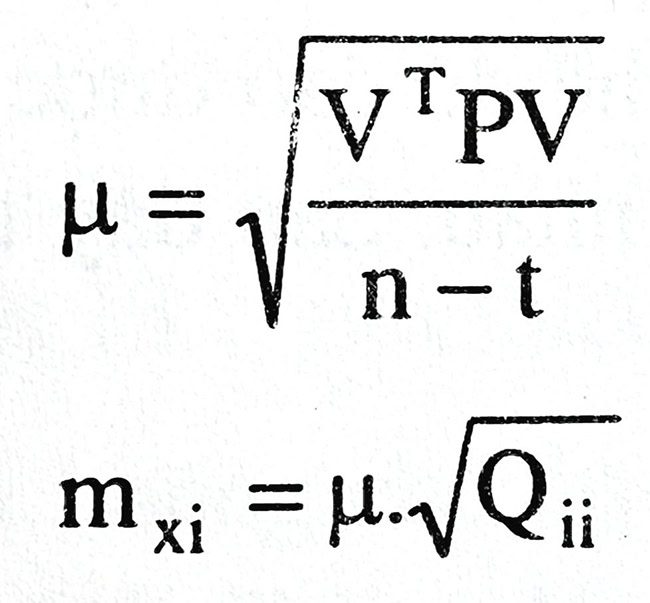Khi bình sai lưới đường chuyền, có nhiều phương pháp có thể sử dụng, tuy nhiên cần chọn được phương pháp có khối lượng tính toán ít và phù hợp với khả năng. Trong bài viết dưới đây, Đất Hợp sẽ giới thiệu về 4 phương pháp bình sai lưới đường chuyền được sử dụng phổ biến nhất!
Bình sai lưới đường chuyền theo phương pháp điều kiện
Khi bình sai lưới đường chuyền theo phương pháp điều kiện trước hết phải xác định đúng số lượng phương trình điều kiện sau đó lựa chọn các điều kiện sao cho chúng độc lập nhau, đúng chủng loại và viết các phương trình càng đơn giản càng tốt.
Sau khi đo lưới đường chuyền ta sẽ xác định được tổng số trị đo n=nβ+nS. Số ẩn cần thiết của bài toán là t đúng bằng hai lần số điểm mới cần xác định tọa độ. Công thức thông thường để xác định số phương trình điều kiện là:
r = n – t
Mặt khác nếu căn cứ vào sơ đồ mạng lưới ta có thể tính số phương trình điều kiện theo công thức:
r = 3P + (Q1 – 1) + 2(Q2 – 1)
Trong đó:
- P: số vòng khép kín
- Q1: số hướng có phương vị chính xác
- Q2: số điểm có tọa độ chính xác
Các phương trình điều kiện gồm rα phương trình điều kiện phương vị và rX phương trình điều kiện tọa độ:
rα = P + Q1 – 1
rX = 2P +2(Q2-1)
Giả sử có lưới đường chuyền như hình bên dưới:
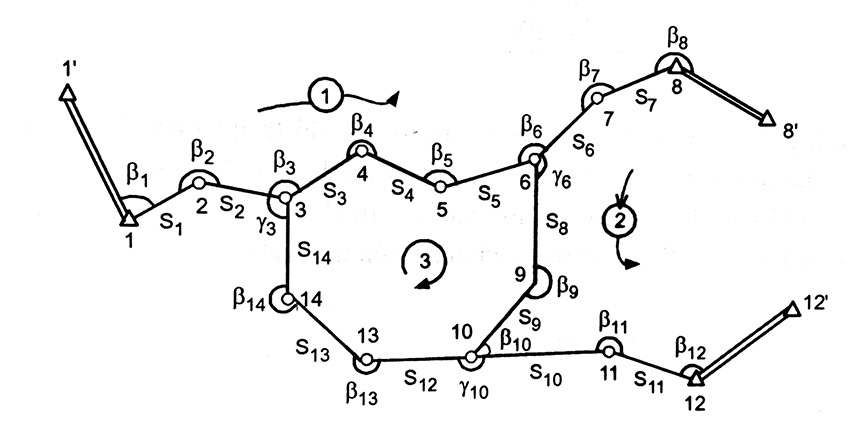
Lưới đường chuyền cần tính toán bình sai (1).
Trong đó đã đo 14 cạnh, 17 góc; biết tọa độ của 3 điểm và 3 hướng của góc phương vị chính xác thuộc lưới cấp cao, số điểm cần xác định là 11. Tổng số phương trình điều kiện sẽ là: r = (17+14) – 2.11 = 9
Mặt khác, theo công thức, ta cũng tính được:
r = 3.1 + (3 – 1) + 2.(3 – 1) = 9
rα = 3
rX = 6
Mạng lưới đường chuyền có thể phân thành 3 tuyến đường chuyền độc lập nhau để thành lập mỗi tuyến 3 phương trình điều kiện.
Tuyến thứ nhất nối 2 điểm 1 và 8, tuyến thứ hai nổi điểm 8 và 12, tuyến thứ ba là vòng khép kín.
Ta có thể lập được 3 phương trình điều kiện cho tuyến thứ nhất:
Đối với mỗi tuyến 2 và 3 ta lập được 3 phương trình điều kiện. Ta có hệ phương trình điều kiện gồm 9 phương trình với 31 trị đo.
Nếu ký hiệu: B là ma trận hệ số phương trình điều kiện có số hàng r = 9, số cột n = 31; V là vectơ số hiệu chỉnh trị đo có số phần tử n = 31; W là vectơ số hạng tự do có số phần tử r = 9, ta có hệ phương trình điều kiện:
BV + W = 0
Từ hệ phương trình điều kiện, ta sẽ lập được hệ phương trình chuẩn số liên hệ:
RK + W = 0
R = BP-1BT
P là ma trận trọng số kết quả đo, khi các trị đo góc và đo cạnh độc lập nhau thì P là một ma trận đường chéo, các phần tử trên đường chéo của nó chính là trọng số các trị đo Pi.
Các phần tử của ma trận P-1 sẽ là 1/Pi = qi
K là vectơ số liên hệ gồm r phần tử.
Giải hệ phương trình ta được các số liên hệ:
K = – R-1W
Số hiệu chỉnh trị đo sẽ tính theo công thức:
V = P-1BTK
Sai số trung phương trọng số đơn vị sẽ tính theo phương pháp thông thường:
Khi cần đánh giá độ chính xác của một yếu tố nào đó trong lưới đường chuyền, ví dụ góc phương vị của một cạnh hoặc tọa độ một điểm bất kỳ, ta lập hàm số trọng số thể hiện quan hệ giữa yếu tố cần đánh giá độ chính xác với trị đo sau bình sai. Tính số nghịch đảo trọng số của hàm 1/PF và tính sai số trung phương của hàm số:
Bình sai lưới đường chuyền theo phương pháp điều kiện kèm ẩn số phụ
Khi bình sai lưới đường chuyền theo phương pháp điều kiện thông thường có các tuyến đường chuyền đồng thời tham gia vào nhiều phương trình điều kiện. Để tránh hiện tượng trùng lặp trên và để cho các phương trình điều kiện của mạng lưới chỉ xuất hiện ở từng đoạn đường chuyền riêng biệt, ta sử dụng phương pháp bình sai điều kiện kèm ẩn số phụ.
Bản chất của phương pháp này là đưa thêm vào bài toán các giá trị sau bình sai của tọa độ xi, yi của các điểm nút và góc phương vị αi của một cạnh tại điểm nút, tức là cứ mỗi điểm nút lại thêm 3 ẩn số phụ. Khi đó các phương trình điều kiện của từng tuyến đường chuyền tách rời nhau.
Cứ mỗi tuyến nối 2 điểm hạng cao, nối một điểm hạng cao tới một điểm nút hoặc nối 2 điểm nối sẽ lập được 3 phương trình điều kiện. Để lập các phương trình điều kiện ta phải cho ẩn số phụ các giá trị gần đúng xi0, yi0, αi0. Sau khi bình sai sẽ tìm được hiệu chỉnh ẩn số vxi, vyi và vαi và tính được trị bình sai:
Xét lưới đường chuyền như hình (1), đo 14 cạnh, 17 góc, có 3 điểm nút và 3 điểm hạng cao có đo nối phương vị. Nếu ta chọn các ẩn số phụ là α3, x3, y3, α6, x6, y6, và α10, x10, y10, thì lưới đường chuyền sẽ tách ra làm 6 tuyến độc lập. Mỗi tuyến được chuyền sẽ lập được 3 phương trình điều kiện.
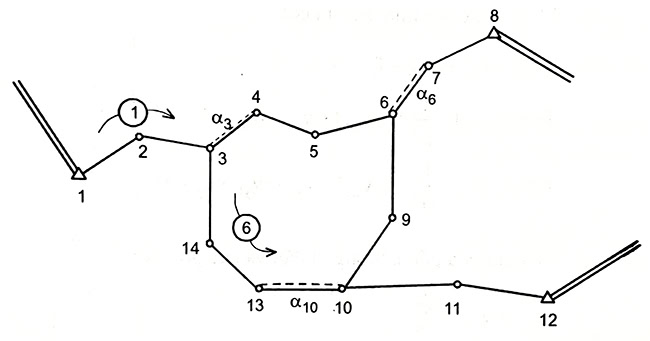
Lưới đường chuyền được tách ra làm 6 tuyến độc lập.
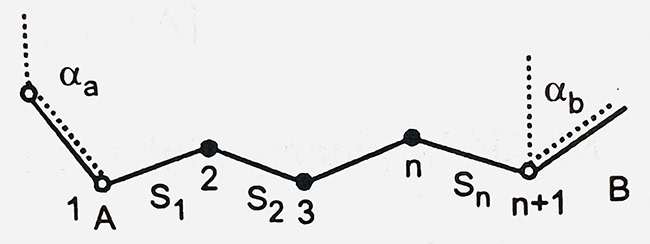
Để tìm hiểu phương pháp thành lập các phương trình điều kiện trong đường chuyền có các ẩn số phụ, ta xem xét đường chuyền nối 2 điểm nút, như hình dưới:
Dạng ban đầu của phương trình điều kiện là:
Trị bình sai của các ẩn số phụ có dạng:
Thay các ẩn số với dạng ban đầu, ta được:
Trong đó:
Thay vΔx, vΔy vào công thức trên ta có:
Số hiệu chỉnh sẽ là hàm của góc phương vị đầu và các góc đo:
Thay vαi vào số hạng thứ 2 của điều kiện tọa độ, ta được:
Thay vαi vào số hạng thứ 2 của điều kiện tọa độ, ta được:
Thay hệ tọa độ trọng tâm đường chuyền vào ta có:
Hệ phương trình trên là dạng cuối cùng của phương trình điều kiện viết cho tuyến đường chuyền nối hai điểm nút A và B với 6 ẩn số phụ.
Bình sai lưới đường chuyền có một điểm nút
Lưới đường chuyền có 4 tuyến đo nối từ 4 điểm đã biết A, B, C và D về điểm nút M.
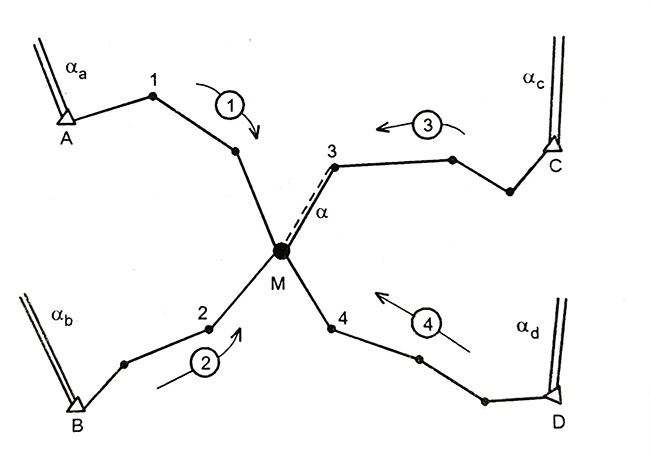
Bình sai lưới đường chuyền có một điểm nút.
Để bình sai chặt chẽ lưới đường chuyền này, ta chọn góc phương vị một cạnh tại M và tọa độ điểm M: α, x, y làm ẩn số. Dùng trị đo một tuyến nào đó tính các trị gần đúng ẩn số α0, x0, y0. Qua bình sai cần tìm các số hiệu chỉnh vα, vx, vy. Phương trình điều kiện kèm ẩn số của một tuyến đường chuyền có dạng sau:
Ứng với mỗi tuyến đường chuyền thì I lần lượt thay là A, B,C, D. Phương trình trên được viết dưới dạng ma trận như sau:
BiVi – EX +Wi = 0 (i = 1, 2 … q)
Các ma trận có dạng:
Từ hệ ma trận trên, ta sẽ lập được hệ phương trình chuẩn như sau:
Rút Ki từ phương trình đầu, thay vào phương trình thứ 2 rồi tính tổng, ta được:
Ta được vectơ ẩn số sau khi bình bình sai sẽ tính dựa theo công thức:
Các vectơ số liên hệ Ki và vectơ số liệu chỉnh Vi của từng tuyến đường chuyền sẽ tính theo công thức:
Cuối cùng, sau khi bình sai ta có được các ẩn số và trị đo:
Bình sai lưới đường chuyền theo phương pháp gián tiếp
Trong phương pháp bình sai gián tiếp có số lượng ẩn số tương đối lớn, nó sẽ bằng hai lần số điểm cần tìm trong lưới khi chọn tọa độ điểm làm ẩn số. Tuy nhiên việc lập các phương trình sai số lại khá đơn giản, mỗi trị đo góc và cạnh sẽ tương ứng với một phương trình sai số. Ma trận hệ số phương trình sai số và hệ số phương trình chuẩn ẩn số là một ma trận rất thưa, có nhiều phần tử bằng không.
Khi thực hiện tính toán bình sai, tận dụng tính thưa của các ma trận để giảm nhẹ khối lượng tính toán. Sau bình sai ta có ngay tọa độ chính xác của các điểm đường chuyền. Ta dễ dàng đánh giá độ chính xác tọa độ điểm sau bình sai cũng như độ chính xác chiều dài cạnh và phương vị các cạnh đường chuyền.
Việc đầu tiên khi bình sai lưới đường chuyền theo phương pháp gián tiếp là xác định đúng số lượng ẩn số và lựa chọn ẩn số. Nếu tổng số điểm trong lưới đường chuyền là P, số điểm cấp cao đã biết tọa độ là Q thì tính được ẩn số theo công thức:
t = 2(P – Q)
Kết hợp mục đích của bài toán bình sai các trị đo và mục đích của việc xây dựng lưới đường chuyền, ta chọn ẩn số là tọa độ xi, yi của các điểm cần xác định.
Giá trị gần đúng của các ẩn số tọa độ xi0, yi0 được xác định thông qua t trị đo cùng các góc phương vị và tọa độ điểm khởi đầu cấp cao. Trong quá trình tính toán tọa độ gần đúng của các điểm đường chuyền cần tính sai số khép tọa độ fx, fy và sai số khép tương đối fs/[s] theo các tuyến đường chuyền khép kín hoặc các tuyến nối 2 điểm cấp cao. Các sai số khép phải nhỏ hơn hạn sai cho phép ứng với từng cấp đường chuyền.
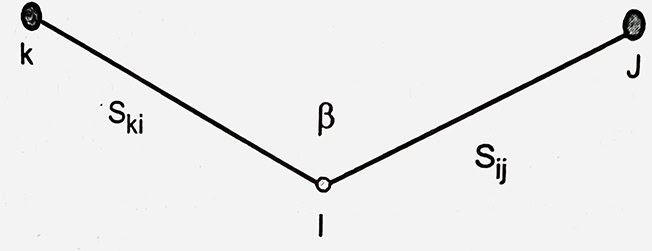
Giả sử có các điểm đường chuyền K, I, J như hình dưới:
Trị đo gồm có góc kij = β và hai cạnh Sik, Sij.
Kí hiệu:
- β, S – trị đo góc và cạnh đường chuyền,
- x0, y0 – trị gần đúng của ẩn số,
- α0, S0 – trị gần đúng của góc phương vị và chiều dài cạnh,
- x, y – trị bình sai của ẩn số,
- β’, S’ – trị bình sai của các góc và cạnh đo,
- ξ. η – số hiệu chỉnh ẩn số sau bình sai,
- vβ, vS – số hiệu chỉnh trị đo sau bình sai,
Ta có các quan hệ:
Từ quan hệ toán học giữa trị đo sau binh sai và các ẩn số sau bình sai ta sẽ lập được các phương trình sai số. Phương trình sai số đối với các trị đo góc sẽ có dạng:
Trong đó:
Phương trình sai số đối với trị đo cạnh sẽ là:
Tập hợp các phương trình sai số ta có hệ phương trình:
AX + L = V
Trong đó:
- A – ma trận hệ số có n dòng và t cột;
- X – vectơ ẩn số có t phần tử;
- L – vectơ số hạng tự do có n phần tử;
- V – vectơ số hiệu chỉnh trị đo có n = nβ + nS phần tử.
Từ hệ phương trình sai số ta lập được hệ phương trình chuẩn:
RX + B = 0
R = ATPA, B = ATPL
Giải phương trình trên ta có:
X = – R-1B = -QB
Tính sai số trung phương trọng số đơn vị và sai số trung phương ẩn số sau bình sai:
Mỗi phương pháp bình sai lưới đường chuyền đều sẽ có những ưu, nhược điểm nhất định. Tùy theo mỗi nhu cầu tính toán bình sai sẽ áp dụng phương pháp phù hợp. Mọi thắc mắc về các phương pháp bình sai lưới đường chuyền, cũng như những vấn đề liên quan ngành trắc địa, hãy liên hệ ngay đến HOTLINE 0903 825 125 để được tư vấn chi tiết!
>>> Xem thêm: 2 bước giúp bình sai lưới khống chế mặt bằng hiệu quả