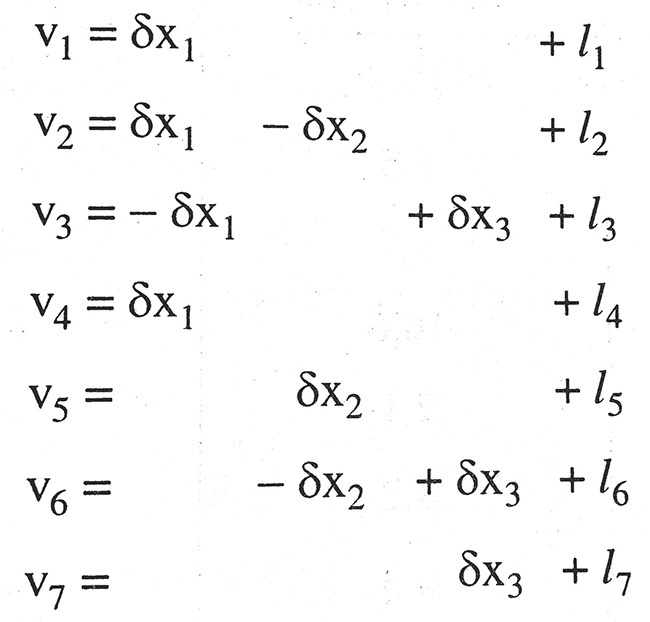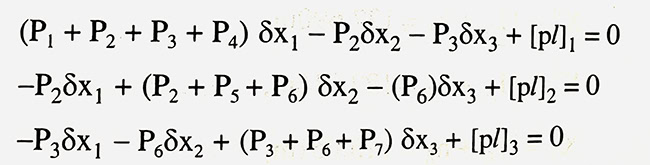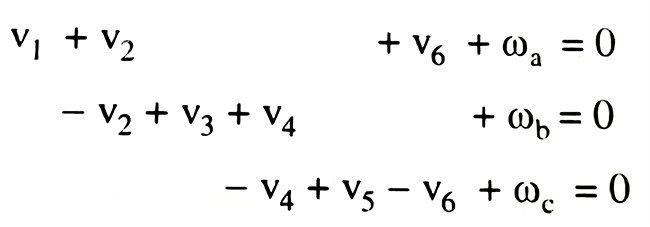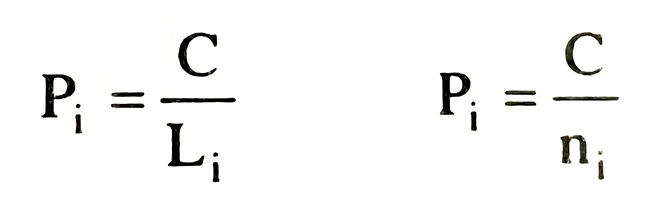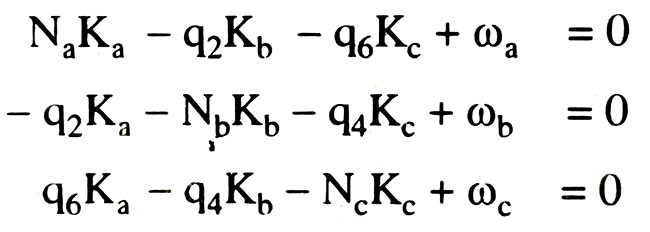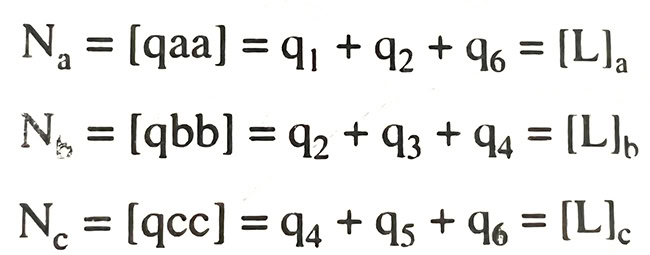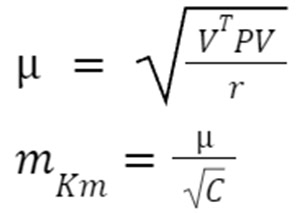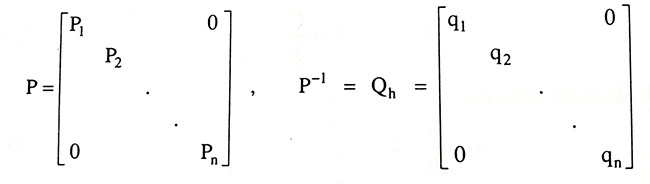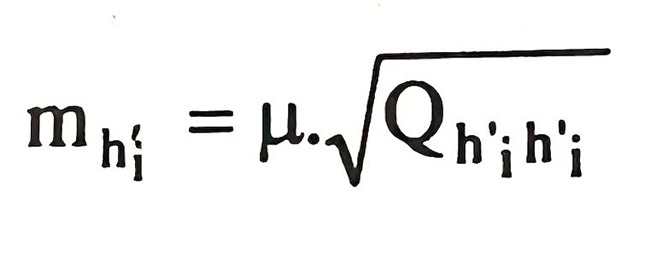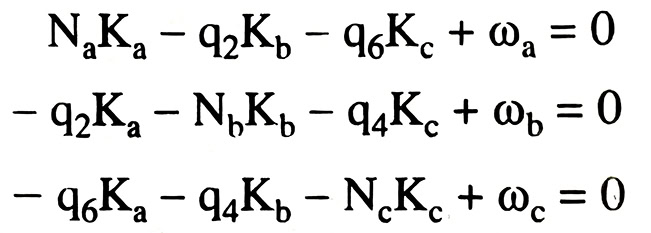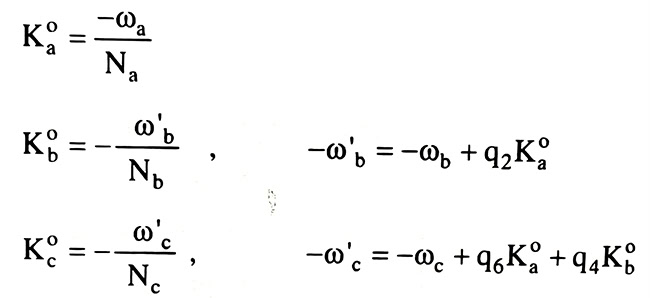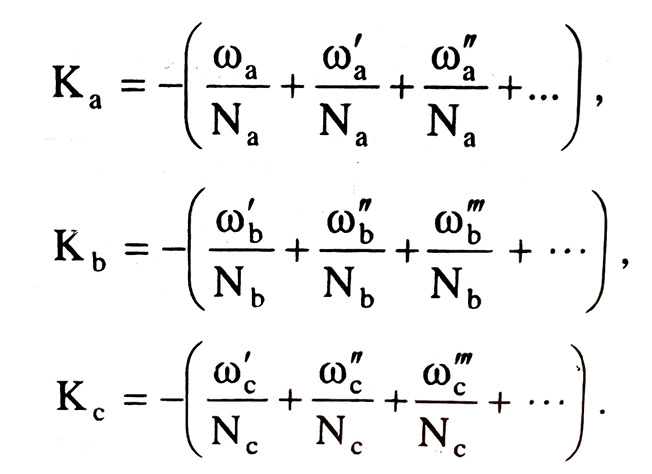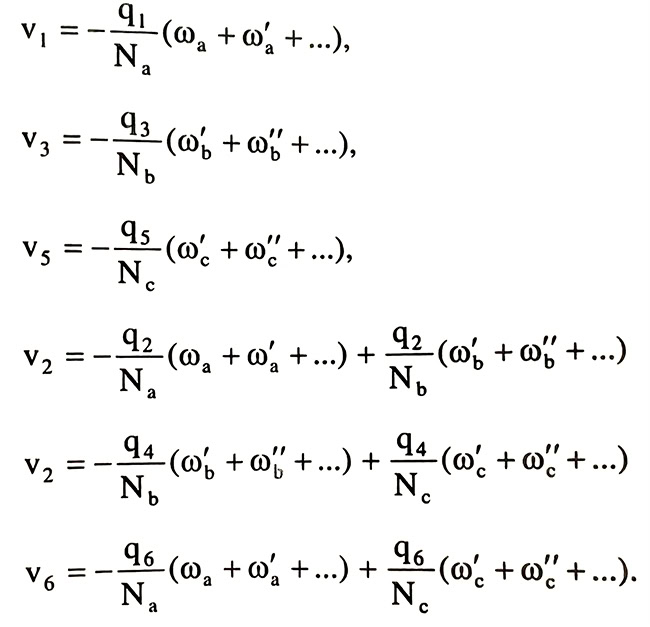Hiện nay có nhiều phương pháp để bình sai lưới thủy chuẩn, tuy nhiên mỗi phương pháp sẽ phù hợp với dạng lưới thủy chuẩn khác nhau. Trong bài viết dưới đây, Đất Hợp sẽ giới thiệu về 3 phương pháp bình sai lưới thủy chuẩn cơ bản.
Bình sai lưới thủy chuẩn theo phương pháp gián tiếp
Bình sai lưới thủy chuẩn theo phương pháp gián tiếp phù hợp để ứng dụng đối với lưới thủy chuẩn dạng phụ thuộc có từ hai điểm nút trở lên.
Đầu tiên, việc quan trọng nhất chính là xác định đúng số lượng và lựa chọn đúng ẩn số cho bài toán. Trong bình sai lưới thủy chuẩn, số ẩn cần xác định chính bằng số điểm mốc chưa biết độ cao.
Có mạng lưới thủy chuẩn hạng III như hình sau, biết độ cao 4 điểm A, B, C và D, có 3 điểm nút N1, N2, N3. Trên các tuyến độ cao từ điểm hạng cao đến điểm nút hoặc tuyến nối 2 nút có các mốc trung gian Ri.
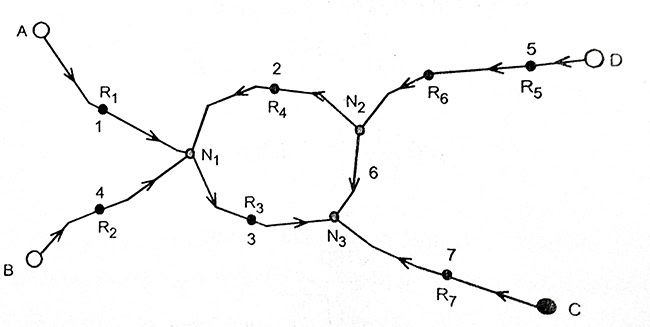
Ví dụ mạng lưới thủy chuẩn hạng III.
Khi bình sai gián tiếp mạng lưới này ta có thể chọn độ cao các nút N và các mốc trung gian R làm ẩn số. Tuy nhiên, để tính toán đơn giản người ta chỉ chọn ẩn số là độ cao điểm nút N. Trị đo đưa vào bình sai không phải là độ chênh cao trên các đoạn nối với các mốc Ri mà là tổng độ chênh cao các tuyến. Sau bình sai cả lưới, tìm được độ cao chính xác của các điểm nút ta sẽ tính được độ cao của các điểm R theo từng tuyến.
Theo cách lựa chọn trên, mạng lưới thủy chuẩn có 7 trị đo và 3 ẩn số là độ cao các điểm nút.
Ký hiệu:
- hi – Độ chênh cao đo được của tuyến thứ i.
- vi – Số hiệu chỉnh trị đo sau bình sai.
- h’i – Độ chênh cao sau bình sai.
- xoj – Trị gần đúng của ẩn số.
- δxj – Số hiệu chỉnh ẩn số.
- xj – Trị bình sai của ẩn số.
Ta có quan hệ:
xj = xoj + δxj
h’i = hi + vi
Hệ phương trình sai số của lưới thủy chuẩn có dạng:
Trọng số trị đo Pi = C/Li
Các hệ số ẩn số trong hệ phương trình đều bằng +1 và -1, từ đó có hệ phương trình chuẩn:
Trong thực tế có thể dựa vào sơ đồ lưới thủy chuẩn tính ngay được ma trận hệ số R = ATPA của hệ phương trình chuẩn theo nguyên tắc:
- Hệ số trên đường chéo chính: được tính bằng tổng trọng số các tuyến có liên quan đến từng điểm nút.
- Hệ số ngoài đường chéo: giá trị bằng -Pi của tuyến có liên quan.
Giải hệ phương trình trên, ra được số hiệu chỉnh ẩn số. Thay vào hệ phương trình sai số, tính được vi và từ đó tính được ẩn số và trị đo sau bình sai.
Bình sai lưới thủy chuẩn theo phương pháp điều kiện
Điều quan trọng khi bình sai lưới thủy chuẩn theo phương pháp điều kiện là phải tính đúng số lượng phương trình điều kiện và lựa chọn các phương trình hoàn toàn độc lập nhau.
Các trị đo đưa vào bình sai là độ chênh cao đo được giữa các điểm mốc. Đại lượng cần xác định chính là độ cao các mốc thủy chuẩn. Số lượng phương trình điều kiện đúng bằng số trị đo thừa và được tính dựa theo công thức tổng quát:
r = n – t
Mặt khác, có thể dựa vào sơ đồ mạng lưới để xác định trực tiếp số lượng và lựa chọn phương trình điều kiện. Nếu trong lưới có P vòng khép kín và có Q điểm đã biết độ cao thì số phương trình điều kiện sẽ là:
r = P + Q – 1 = 3 + 1 – 1 = 3
Giả sử có lưới thủy chuẩn như hình dưới, biết độ cao điểm A, đo 3 tuyến, cần xác định độ cao 3 điểm mốc R1, R2 và R3. Ta có số phương trình điều kiện: r = n – t = 6 – 3 = 3.
Chọn 3 vòng khép kín và chiều tính sai số khép thuận theo chiều đồng hồ (phải sang trái), lập được 3 phương trình điều kiện số hiệu chỉnh:
Trọng số trị đo tính theo chiều dài tuyến đo hoặc số trạm máy:
Số nghịch đảo trọng số trị đo: qi = 1/Pi = Li
Hệ phương trình điều kiện số hiệu chỉnh có thể viết ở dạng: BV + W = 0
Hệ phương trình chuẩn số liên hệ:
NK + W = 0
N = BP-1BT
Các hệ số của phương trình điều kiện chỉ có giá trị +1 hoặc -1 nên từ sơ đồ lưới suy ra ngay được hệ phương trình chuẩn:
Trong đó:
Tiếp tục giải bài toán ta có:
K = -N-1W
V = P-1BTK
Tính các sai số đặc trưng theo công thức:
Trị đo sau bình sai sẽ tính theo công thức: h’ = h + v
Độ chính xác trị đo hi được đặc trưng bởi trọng số Pi. Vectơ trị đo h có ma trận trọng số P và có ma trận trọng số đảo P-1, đó là các ma trận đường chéo:
Các trị đo sau bình sai h’i là các đại lượng phụ thuộc lẫn nhau. Ma trận tương quan đặc trưng cho sự phụ thuộc giữa các trị đo sau bình sai được xác định theo công thức:
Qh’ = P-1 – P-1BTN-1BP-1
Dựa vào ma trận Qh’ ta có thể tính sai số trung phương trị đo sau bình sai hi’:
Bình sai lưới thủy chuẩn theo sơ đồ (phương pháp Popov)
Phương pháp bình sai lưới thủy chuẩn trực tiếp trên sơ đồ do nhà trắc địa Popov đề ra, đây được xem là phương pháp tính toán dễ thực hiện và đơn giản. Phương pháp này dựa trên cơ sở lý thuyết bình sai điều kiện, đối với phần giải hệ phương trình chuẩn số liên hệ và tính số hiệu chỉnh trị đo được tính đúng dần.
Từ lưới thủy chuẩn, ta có hệ phương trình điều kiện và hệ phương trình chuẩn như sau:
Lần lượt từ phương trình trên, giá trị gần đúng của số liên hệ K là:
Thay các giá trị gần đúng của Kio vào từng phương trình ta có các sai số khép mới ω’i rồi ω”i ta sẽ tính được các số hiệu chỉnh ΔK’i rồi ΔK’’i. Tổng quát ta có số liên hệ K tính theo công thức đúng dần:
Các số hiệu chỉnh sẽ tính theo công thức:
vi = qi(aiKi +biKb + ciKc)
Ta có:
Đối với phương pháp bình sai lưới thủy chuẩn trực tiếp trên sơ đồ:
- Các hệ số ở vế phải công thức trên chính là các tỷ lệ phân phối sai số khép lần thứ j cho đường đo thứ i tính tỷ lệ theo chiều dài Li hoặc số trạm máy ni.
- Tuyến đo nào liên quan đến 1 điều kiện thì số hiệu chỉnh của nó chỉ do sai số khép 1 vòng phân phối cho. Về giá trị lấy tổng các phần được phân phối lặp còn dấu thì lấy ngược dấu sai số khép.
- Những tuyến liên quan đến hai điều kiện vòng khép thì số hiệu chỉnh của nó gồm hai phần do hai vòng phân phối cho. Trước tổng sẽ lấy dấu trừ nếu chiều đo cùng chiều sai số khép. Trước tổng sẽ lấy dấu cộng nếu chiều đo ngược với chiều tính sai số khép.
Sau khi tính được các số hiệu chỉnh trị đo vi ta tính trị đo sau bình sai và tính các sai số đặc trưng.
Với mỗi phương pháp bình sai lưới thủy chuẩn đều có những điểm khác biệt, do đó tùy theo nhu cầu tính toán bình sai sẽ áp dụng phương pháp phù hợp. Mọi thắc mắc về các phương pháp bình sai lưới thủy chuẩn, cũng như những vấn đề liên quan ngành trắc địa, hãy liên hệ ngay đến HOTLINE 0903 825 125 để được tư vấn chi tiết!
>>> Xem thêm: 4 phương pháp bình sai lưới đường chuyền